本文以我国沪深两市2005年90家上市公司作为研究对象,以其被ST前一年的截面数据建立一套财务指标体系,应用Logistic 回归和BP神经网络方法建立财务危机预警模型, 进行了实证研究。
一、笔者对财务危机的界定
如何界定财务危机是进行财务预警研究考虑的首要问题。国外大部分研究将企业在破产法下提出破产申请的行为作为确定企业进入财务危机的标志,Altman (1968)指出财务危机分4种类型:经营失败、无偿付能力、违约、破产;Deakin (1972)认为财务危机公司是指已经破产、无力偿还债务而已经进行清算的公司;ROSS等人(1999)认为可从4个方面定义企业的财务危机:企业失败、法定破产、技术破产和会计破产。由于我国证券市场发育不够成熟,缺乏健全的退市机制,上市资格一直受到证监会的严格控制,巨大的需求使业绩差的“壳资源”上市公司炙手可热,即便处于破产的边缘,也会被完全吸收。故而,结合我国的实际情况,笔者把公司被特别处理(ST)作为陷入财务困境的标志,ST制度是对“状况异常”的上市公司实行股票交易的特别处理。笔者在研究中将财务危机确切界定为公司财务状况异常而被“特别处理”。
二、国内外文献综述
目前,研究财务预警的模型主要集中于以下几类模型:单变量模型、多变量统计分析模型和人工神经网络模型。
(一)单变量模型
该模型研究的先驱者美国芝加哥大学教授WilliamBeaver (1966)提出了较为成熟的单变量模式,他以79家失败企业和相同数量、同等规模成功企业为样本,通过研究个别财务比率长期走势预测企业面临危机情况;我国学者陈静(1999)以1998年的27家ST和27家非ST公司,利用1995-1997年的财务报表数据进行了单变量分析,提出流动比率和负债比率误判率最低;吴世农、卢贤义(2001)以70家ST和70家非ST上市公司为样本,应用单变量分析研究财务困境出现前五年内这两类公司21个财务指标各年的差异,最后确定了6个预测指标。
(二)多变量统计分析模型
多变量统计分析模型同单变量模型相比,更全面地反映了企业的财务状况。由于建模使用的统计方法不同,又分为多元回归分析模型、多元判别分析模型、主成分分析模型和Logisitic回归模型。美国学者Edward Altman教授率先将多元线性判别方法引入财务预警领域,开创了多变量预警模型的先河,提出Z-score模型;张玲(2000)选取沪深两市14个行业120家上市公司为样本,从偿债能力、盈利能力、资本结构状况和营运状况4个方面15个相关财务比率中筛选出4个变量构建了二分类线性判定模型;周首华(1996)构建了F分数模型。其中Logisitic回归模型已经引起人们的高度关注。
(三) 人工神经网络模型
人工神经网络(ANN)的发展始于20世纪40年代,它利用大量非线性并行处理关系来模拟众多的人脑神经元的运作,具有较好的模式识别、学习、训练和容错能力,克服了传统统计方法的局限。M.Odom(1990)最早把人工神经网络应用于财务危机预测研究;由Rumelhart和McClelland(1986)提出的一种多层前馈网反向传播BP神经网络方法,适用于模拟输入、输出的近似关系,而且具有无限隐含层节点的三层BP网络可以实现任意从输入到输出的非线性映射,同时也是近年来应用最广泛最成熟的ANN模型;Lapedes和Fayber(1987)首次运用神经网络模型对银行信用风险进行了预测和分析;Trippi和Turban(1992)对美国银行财务危机进行了分析;我国学者杨保安(2001)选取15个财务指标,运用BP神经网络方法建立了供银行进行授信评价的预警系统。
三、实证研究
笔者主要根据Logisitic回归模型和BP神经网络模型理论,搜集上市公司的财务数据,建立不同的实证模型进行比较,分析财务预警的效果。
(一)研究样本的设计
笔者将我国上市公司中的ST公司界定为“财务失败”。选取了2005年沪深上市的30家ST公司和同行业相近规模的30家非ST公司作为估计样本组,另外选取同时期的30家ST公司和非ST公司作为测试样本组。估计样本组的数据用于构建预警模型,而测试样本组用于检验预警模型的有效程度。鉴于研究的需要,所选取的财务指标数据是ST公司被宣布特别处理前一年(2004)的年报数据,样本公司的财务数据主要来自巨潮咨讯网站和中国上市公司咨讯网站统计年鉴。
(二)财务指标体系的选择
财务比率的选取是构建财务危机预警模型极其重要的一步,选择的恰当与否关系到财务危机预警模型的有效性。笔者采用定性分析和定量分析相结合的方法, 借鉴国内外学者的实证研究成果并结合我国上市公司的实际情况, 从企业的市场价值指标、盈利能力、偿债能力、经营能力、成长能力、资本结构等6个方面, 提供了17个备选财务指标,作为研究模型中使用的初始变量,如表1所示:
表1 备选财务预警指标
| 市场价值指标 | 盈利能力 | 偿债能力 | 经营能力 | 成长能力 | 资本结构 |
| 每股收益 每股净资产 |
总资产报酬率 净资产收益率 主营业务利润率 销售毛利率 销售净利率 |
流动比率 速动比率 |
总资产周转率 应收账款周转率 股东权益周转率 存货周转率 |
总资产增长率 主营业务 收入增长率 |
资产负债率 股东权益比率 |
然而,模型中包括如此多的指标是不经济的,同时由于财务指标之间的相关性比较强,结构错综复杂,因此在建立模型前有必要对初始变量进行筛选。ST公司和非ST公司之间应该具有显著差别,进入预警模型的变量至少能有效、显著地区别ST公司和非ST公司,这是入选变量的必要条件。所以笔者采用统计分析法中的显著性检验方法(T检验)对预警指标进行第一次筛选。使用SPSS统计分析软件,对财务危机企业被处理前一年(2004)的数据进行显著性检验。从T检验结果可以看出,选取显著性水平为0.05,在备选的17个财务预警指标中, 总资产报酬率(X1)、净资产收益率(X2)、流动比率(X3)、速动比率(X4)、资产负债率(X5)、股东权益比率(X6)、总资产周转率(X7)、总资产增长率(X8)、每股收益(X9)、每股净资产(X10)的双尾检验的显著概率均小于0.05,通过了显著性检验,说明这些指标变量在ST公司和非ST公司之间是有显著差异的,因此选取这10个变量进入预测模型。
(三)Logistic回归分析模型
以60家估计样本财务危机发生前一年的数据为基础,使用筛选的10个指标为自变量,构建Logistic回归分析模型,运用SPSS软件分析获得模型的系数及相关参数见表2.
表2 估计样本Logistic回归模型参数表
| B | S.E. | Wald | df | Sig. | Exp(B) | ||
| Step 1(a) | 每股净资产 | 1.779 | .487 | 13.348 | 1 | .000 | 5.921 |
| Constant | -2.326 | .723 | 10.353 | 1 | .001 | .098 | |
| Step 2(b) | 总资产周转率 | .051 | .024 | 4.368 | 1 | .037 | 1.052 |
| 每股净资产 | 1.674 | .560 | 8.922 | 1 | .003 | 5.333 | |
| Constant | -2.496 | .902 | 7.664 | 1 | .006 | .082 | |
a Variable(s) entered on step 1:每股净资产 b Variable(s) entered on step 2:总资产周转率
注:B为预警变量的回归系数:S.E. 为回归系数的标准误差;Wald是检验偏回归系数的统计盈;df为自由度;Sig.为显著水平。
从表中可以看出,X7和X10变量的显著水平均小于0.05,说明预测能力较强,现构建Logistic回归模型,其方程表示为: Logit(Y)=Ln(P/1-P)=-2.496 + 0.051X7+1.674X10.
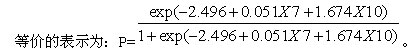
P(Y=1)代表公司发生财务危机的概率, P(Y=0)代表公司不发生财务危机的概率,因此笔者以P=0.5为最佳判别点,以期能使预警模型在实际中有更好的预测效果。当P大于0.5时,判别为ST公司,数值越大,表明该公司未来一年内发生财务危机的可能性越大;当P小于0.5时,判别为非ST公司,数值越小,表明该公司财务状况越安全;当P等于0.5时,说明该公司的财务状况不太明显,但也判别为ST公司。
(四)BP神经网络模型
笔者采用三层BP网络,由输入层、隐含层、输出层组成。输入层至隐含层以及隐含层至输出层的传输函数均选用非线性S 型Sigmoid 函数,这个算法的学习过程由正向和反向传播过程组成。
运用软件Matlab 6.5, 构建了10-16-1的三层BP网络,并选取了60个训练样本和30个测试样本进行实验。另外,由于输入是连续变量,输出是布尔型离散向量, 训练或测试前使用Matlab的Premnmx函数对样本进行归一化处理,作为网络的输入数据。BP神经网络的设计包括输入层、隐含层、输出层、传递函数、训练函数等网络结构和网络参数的设置,具体到文本的研究,设置如下:
1.输入层:输入层神经元个数由输入量决定,确定了10个输入节点。
2.输出层:输出层神经元的个数由输出类别决定。具体到本文,网络的输出层定义为一个节点,即上市公司的实际财务状况。在训练样本集中,样本的输出向量为T(当为ST公司时,T=1;当为非ST公司时,T=0)。
3.隐含层:关于隐节点数的选取至今尚未找到一个很好的解析式来表示,过少,将影响到网络的有效性;过多,则会大幅度增加网络训练的时间,用于模式识别的BP网络,根据经验,可以参照以下公式进行设计:n=n1+0.618×(n1- n2)其中,n为隐节点数,n1为输入节点数,n2为输出节点数。由此公式选取隐含层节点数为16.笔者采用隐含层神经元个数为16个。
4.传递函数:传递函数的好坏对一个神经网络的训练效率至关重要。考虑到输出层的期望输出数据为0或1,经反复测试,笔者对输入层到隐含层的传递函数确定为正切函数tansig(n),它将神经元的输入范围从(- ,+ )映射到(1,-1),隐含层到输出层之间的传递函数确定为对数函数logsig(n),它将神经元的输入范围从(- ,+ )映射到(0, 1)。
5.网络参数:目标误差0.001,学习速率为0.01,训练循环次数1000次。学习率通常在0.01~0.9之间。一般来说,学习率越小,训练次数越多, 但学习率过大,会影响网络结构的稳定性。误差通常需要根据输出要求来定, e越低, 说明要求的精度越高。
6.训练函数:本文选取基于快速BP算法的训练函数trainlm借助Matlab6.5语言编程实现模型在PC上经过75个训练周期后达到要求。
(五)不同模型结果比较
表3 不同模型的判别准确率比较
| 模型名称 | 估计样本准确率 | 测试样本准确率 | ||||
| 总 体 | ST | 非ST | 总 体 | ST | 非ST | |
| Logistic回归模型 | 86.7% | 86.7% | 86.7% | 83.3% | 80% | 86.7% |
| BP神经网络模型 | 99% | 98% | 100% | 90% | 93.3% | 86.7% |
从上述两种模型之间的判别准确率比较表可以明显看出,估计样本方面BP神经网络判别效果高于Logisitic模型;测试样本方面两者相当。
四、研究结论及局限性
笔者在回顾国内外财务预警模型经典文献和研究成果的基础上,以我国沪深90家上市公司为研究对象,利用Logisitic回归模型和BP神经网络方法进行了实证研究。
(一)研究结论如下
1.我国上市公司的财务指标包含着预测财务困境的信息含量,因此利用公司的财务比率可以预测其是否陷入财务困境。在上市公司陷入财务危机的前一年,笔者所选的17个财务指标中10个具有判定和预测财务困境的信息含量,这些指标涵盖了反映公司财务状况的各方面因素,说明建立指标体系是合理恰当的。2.中国证监会对上市公司中ST的定义是有效的,因为笔者证明了上市公司的ST板块与非ST板块有显著的区别,能用各种判别模型加以区分。3.研究采用的两种模型方法都可以进行公司财务困境预测研究,但判定效果存在差异。
(二)研究存在着一定的局限性
1.鉴于数据收集的限制,笔者选取的都是上市公司的财务数据,不适用于大量的小型公司。
2.笔者的研究是以上市公司真实财务指标为前提假设的,不能排除目前我国上市公司会计信息失真现象的存在。
3.由于反映公司财务状况的指标很多,可能漏掉一些重要的比率,得出的结果不够完善。
4.笔者研究的是上市公司的截面数据,没有考虑到ST前一年或两年的情况,势必会影响实证结果。


