新用户扫码下载
扫码下载APP
及时接收考试资讯及
备考信息
Determining interest rate forwards and their application to swap valuation
The previous article on bonds, published in the September 2011 issue of
Student Accountant, considered the relationship between bond prices, the yield
curve and the yield to maturity. It demonstrated how bonds can be valued and
how a yield curve may be derived using bonds of the same risk class but of
different maturities. It also showed how individual company yield curves may
be estimated.
This article follows on from that, and will show how interest rate forwards may
be determined from the spot yield curve. It will then briefly discuss what they
mean, before proceeding to show how they may be used in determining the
value of an interest rate swap. The second article addresses the learning
required in the F1 and F3 areas of the Paper P4 Syllabus and Study Guide.
DETERMINATION OF INTEREST RATE FORWARDS
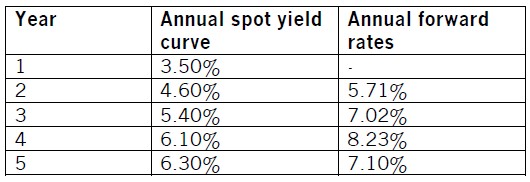
Supposing that a bank assesses and quotes the following rates to a company,
based on the annual spot yield curve for that company’s risk class:
One-year 3.50%
Two-year 4.60%
Three-year 5.40%
Four-year 6.10%
Five-year 6.30%
This indicates that the company would have to: pay interest at 3.50% if it
wants to borrow a sum of money for one year; pay interest at 4.60% per year if
it wants to borrow a sum of money for two years; pay interest at 5.40% per
year if it wants borrow a sum of money for three years; and so on.
Alternatively, for a two-year loan, the company could opt to borrow a sum of
money for only one year, at an interest rate of 3.50%, and then again for
another year, commencing in one year’s time, instead of borrowing the money
for a total of two years.
Although the company would be uncertain about the interest rate in one year’s
time, it could request a forward rate from the bank that is fixed today – for
example, through a 12v24 forward rate agreement (FRA). The question then
arises: how may the value of the 12v24 FRA be determined?
A forward rate commencing in one year for a borrowed sum lasting a year can
be calculated as follows:
The compound factor for the total interest rate for two years = 1.0462
The compound factor for the one-year interest rate = 1.035
The one-year forward interest rate can be calculated as follows:
1.04602 / 1.0350 = 1.0571 or 5.71%
The interest rate forward commencing in one year for a borrowed sum lasting a
year would be 5.71%. The 12v24 FRA = 5.71%.
Similarly, annual interest rate forward rates for future years can be calculated
as follows:
The interest rate forward starting in year 3, for a year (24v36 FRA) =
1.05403 / 1.04602 = 1.0702 or 7.02%
[or: 1.05403 / (1.0350 x 1.0571)]
The interest rate forward starting in year 4, for a year (36v48 FRA) =
1.06104 / 1.05403 = 1.0823 or 8.23%
[or: 1.06104 / (1.0350 x 1.0571 x 1.0702)]
The interest rate forward starting in year 5, for a year (48v60 FRA) =
1.06305 / 1.06104 = 1.0710 or 7.10%
[or: 1.06305 / (1.0350 x 1.0571 x 1.0702 x 1.0823)]
In summary:
Supposing the company wants to borrow a sum of money for three years on
the basis of the above rates:
i. it could pay annual interest at a rate of 5.40% in each of the three
years, or
ii. it could pay interest at a rate 3.50% in the first year, 5.71% in the
second year and 7.02% in the third year, or
iii. it could pay annual interest at a rate of 4.60% in each of the first two
years and 7.02% in the third year.
USING INTEREST RATE FORWARDS TO VALUE A SIMPLE INTEREST RATE SWAP CONTRACT
Supposing the above company has $100m borrowings in the form of variable
interest rate loans repayable in five years and pays interest based on the above yield curve. It expects interest rates to increase in the future and is therefore keen to fix its interest rate payments.
The bank offers to swap the variable interest rate payments for a fixed rate,
such that the company pays a fixed rate of interest to the bank in exchange for
receiving a variable rate of return from the bank based on the above yield rates
less 50 basis points. The variable rate receipts from the bank will then be used
to pay the interest on the loan.
The fixed equivalent rate of interest the company will pay the bank for the swap can be calculated as follows:
The current expected amounts of interest the company expects to receive from
the bank, based on year 1 spot rate and years 2, 3, 4 and 5 forward rates are:
Year 1 0.0300 x $100m = $3.00m
Year 2 0.0521 x $100m = $5.21m
Year 3 0.0652 x $100m = $6.52m
Year 4 0.0773 x $100m = $7.73m
Year 5 0.0660 x $100m= $6.60m
Note: The rates used to calculate the annual amounts are reduced by 50 basis
points or 0.5%.
At the start of the swap, the net present value of the swap receipts based on
the variable rates from the bank will be the same as the costs based on the
fixed amount paid to the bank.
Let’s say R is the fixed amount of interest the company will pay the bank, then
($3.00m – R) x 1.035-1 +
($5.21m – R) x 1.046-2 +
($6.52m – R) x 1.054-3 +
($7.73m – R) x 1.061-4 +
($6.60m – R) x 1.063-5
= 0
Removing the brackets, the above expands to:
2.90m – 0.966R + 4.76m – 0.914R + 5.57m – 0.854R +
6.10m – 0.789R + 4.86m – 0.737R= 0
Simplifying this, adding all the $ flows together and R-flows together, gives:
24.19m – 4.26R = 0
$5.68m = R
In percentage = $5.68m/$100m = 5.68%
In practice the receipts and payments of the swap would be netted off such
that the company will expect to pay $2.68m ($5.68m – $3.00m) to the bank in
year one, and expect to receive $0.84m ($6.52m – $5.68m) from the bank in
year three, and so on for the other years. The present values of these net
annual flows, discounted at the yield curve rates, will be zero. The fixed rate of
5.68% is lower than the five-year spot rate of 6.30% because some of the
receipts and payments related to the swap contract occur in earlier years when
the spot yield curve rate is lower.
Although at the commencement of the contract, the present value of the swap
is zero, as interest rates fluctuate, the value of the swap will change. For
example, if interest rates increase and the company pays interest at a fixed
rate, then the swap’s value to the company will increase. The value of the swap contract will also change as the swap approaches maturity, and the number of receipts and payments reduce.
CONCLUSION
The previous article and this article considered the relationship between
bonds, interest rates, spot and forward yield curves, culminating with how the
forwards rates can be used to determine the equivalent fixed rate of a simple
swap contract. The examples used were simplified into annual cash flows and
rates, and students undertaking Paper P4 should be able to demonstrate their
knowledge and understanding of these areas to this extent.
In practice, valuation of bonds and related products is more complicated
because of factors such as: cash flows occurring more frequently than once a
year, early redemption of products, change in product values, and so on.
However, these aspects are beyond the scope of the Paper P4 syllabus.
Shishir Malde is examiner for Paper P4
【我要纠错】 责任编辑：Sarah
推荐阅读
相关资讯
新用户扫码下载
京公网安备 11010802044457号